Wave properties

4.5.1 Describe the reflection and transmission of waves at a boundary between two media.

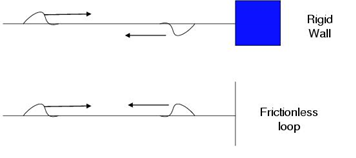
Figure 4.5.1 - Transmission of waves

When fixed, the wave is reflected and inverted. When free, the wave is reflected.

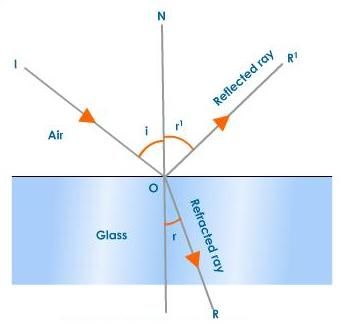
Figure 4.5.2 - Reflection and refraction of waves

When the wave meets the boundary between two different mediums it is partially reflected and partially refracted.

4.5.2 State and apply Snell?s law.

The refraction indices, n, represent the factor by which light is slowed down within a refractive medium compared to its velocity in vacuum.

4.5.3 Explain and discuss qualitatively the diffraction of waves at apertures and obstacles.

When waves pass through an aperture they tend to spread. This is similarly the case with obstacles. This wave property is known as diffraction. For there to be diffraction the wavelength needs to be of the same order of magnitude as the aperture width. This becomes more important as the wavelength of the wave is large as compared to the aperture width.

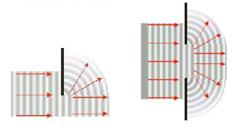
Figure 4.5.3 - Diffraction of waves

4.5.4 Describe examples of diffraction.

Diffraction is the reason to why we can still hear sounds of objects without seeing them. You can hear the TV from upstairs in your room if it is loud enough.

4.5.5 State the principle of superposition and explain what is meant by constructive interference and by destructive interference.

The principal of superposition states that when two waves meet the resultant displacement is the sum of the individual displacements.

Constructive interference occurs when two pulses displaced in the same direction cause an overlap. The resultant displacement is the sum of both displacements.

Destructive interference occurs when two pulses displaced in opposite directions  cause an overlap. The resultant displacement is the difference of both displacements.

4.5.6 State and apply the conditions for constructive and for destructive interference in terms of path difference and phase difference.

Constructive interference is when two waves are In phase. By that we mean the path difference between the two waves is zero

Destructive interference is when the two waves are out of phase.

4.5.7 Apply the principle of superposition to determine the resultant of two waves.