Kinematics
2.1.1 Define displacement, velocity, speed and acceleration.
Displacement
Displacement is the distance moved in a particular direction. It is a vector quantity.
SI unit: m
Symbol: s
Velocity
Velocity is the rate of change of displacement. It is a vector quantity.
Velocity = (change in displacement / change in time)
SI unit: m s-1
Symbol: v or u
Speed
Speed is the rate of change of distance. It is a scalar quantity.
Speed = (change in distance / change in time)
SI unit: m s-1
Symbol: v or u
Note that speed and velocity are not the same thing. Velocity has a direction.
Acceleration
Acceleration is the rate of change of velocity. It is a vector quantity.
Acceleration = (change in velocity / change in time)
SI unit: m s-2
Symbol: a
Note that acceleration is any change in velocity, meaning an increase or decrease in velocity or a change in direction.
2.1.2 Explain the difference between instantaneous and average values of speed, velocity and acceleration.
Instantaneous
An instantaneous value of speed, velocity or acceleration is one that is at a particular point in time.
Average
An average value of speed, velocity or acceleration is one that is taken over a period of time.
2.1.3 Outline the conditions under which the equations for uniformly accelerated motion may be applied.
The equations of uniformly accelerated motion can only be under conditions where the acceleration is constant.
The equations of uniformly accelerated motion are as follows:
| Variable | Symbol |
| t | time taken |
| s | distance travelled |
| u | initial velocity |
| v | final velocity |
| a | acceleration |
Table 1.2.1 - Variables used in uniformly accelerated motion equations
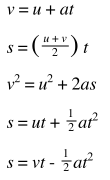
Other equations may be derived from these equations.
2.1.4 Identify the acceleration of a body falling in a vacuum near the Earth?s surface with the acceleration g of free fall.
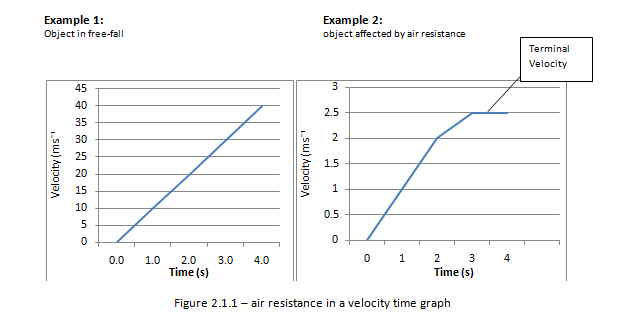
When we ignore the effect of air resistance on an object falling down to earth due to gravity we say the object is in free fall. Free fall is an example of uniformly accelerated motion as the only force acting on the object is that of gravity.
On the earths surface, the acceleration of an object in free fall is about 9.81 ms-1. We can easily recognise the uniform acceleration in displacement - time, velocity - time and acceleration - time graphs as shown below:
2.1.5 Solve problems involving the equations of uniformly accelerated motion.
A car accelerates with uniformly from rest. After 10s it has travelled 200 m.
Calculate:
Its average acceleration
S = ut + 1/2 at²
200 = 0 x 10 + 1/2 x a x 10²
200 = 50a
a = 4 m s-2
Its instantaneous speed after 10s
v² = u ² + 2as
= 0 + 2 x 4 x 10
= 80
V= 8.9 m s-1
2.1.6 Describe the effects of air resistance on falling objects.
Air resistance eventually affects all objects that are in motion. Due to the effect of air resistance objects can reach terminal velocity. This is a point by which the velocity remains constant and acceleration is zero.
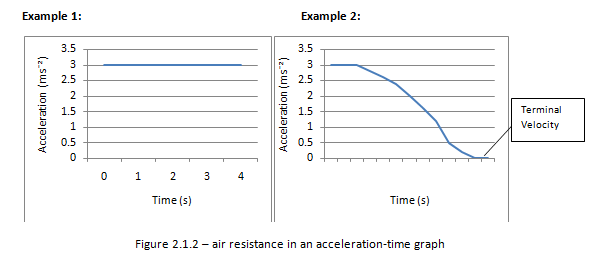
In the absence of air resistance all objects have the same acceleration irrespective of its mass.
2.1.7 Draw and analyse distance?time graphs, displacement?time graphs, velocity?time graphs and acceleration?time graphs.
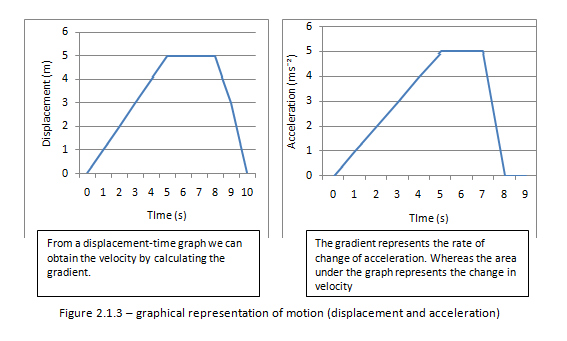

2.1.8 Calculate and interpret the gradients of displacement?time graphs and velocity?time graphs, and the areas under velocity?time graphs and acceleration?time graphs.
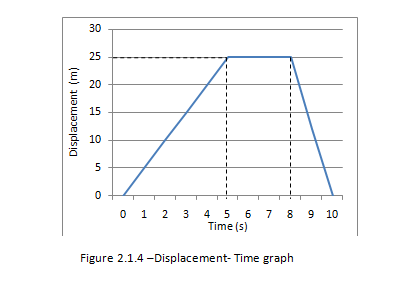
Determining its velocity
We know that the gradient of a displacement – time graph gives us its velocity. Therefore for the first 5 seconds the speed is:
25/5 =5ms?¹
After the first 5 s the object is stationary for 3 s. For these 3s its velocity is zero.
After 8s the object starts to return at a faster speed then before. From the graph we find the speed to be:
25/2 =12.5ms?¹
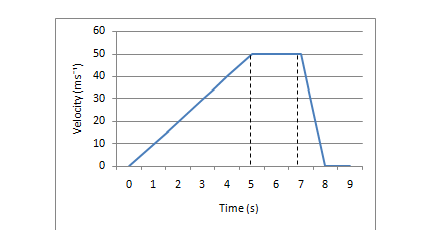
Figure 2.1.5 – Velocity -Time graph
Determine its acceleration
We know that the gradient of a velocity- Time graph gives us its acceleration. Therefore for the first 5 s the acceleration is:
50/5 =10 ms?²
When the object is at constant speed from 5s to 7s its acceleration is zero. During the last second of the objects journey the object is decelerating at:
50/1 =50 ms?²
Determine its displacement
The area under a velocity-time graph is the displacement. During the first 5 s the object has travelled:
½ x 5 x 50 = 125m
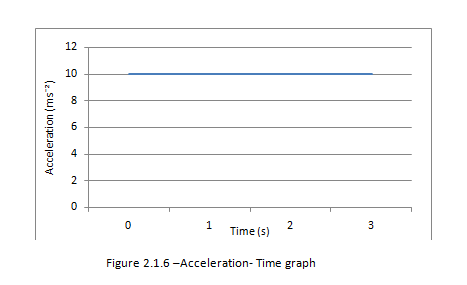
Determine the change in velocity
The area under the acceleration- Time graph gives us the change in velocity
From the graph we find that the change in velocity is 10 x 3 = 30 ms?¹
Note: The gradient of the acceleration - time graph is actually the rate of change of acceleration. However it isn’t often useful.
