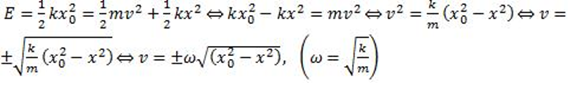Kinematics of simple harmonic motion (SHM)

4.1.1 Describe examples of oscillations.

• A pendulum

• A mass attached to a spring attached to a wall that oscillates back and forth.

4.1.2 Define the terms displacement, amplitude, frequency, period and phase difference.

Displacement - The instantaneous distance of the moving object from its mean position

Amplitude - The maximum displacement achievable from the mean position

Frequency - The number of oscillations completed per unit time

F = 1/t

Period - the time taken for a complete oscillation

T = 1/f

Phase difference - the measure of how "in step" different particles are. If they are moving together they are said to be in phase. If not they are said to be out of phase.

4.1.3 Define simple harmonic motion (SHM) and state the defining equation as a=-ω²x.

Simple harmonic motion is defined as the motion that takes place when the acceleration, a , is always directed towards and is proportional to its displacement from a fixed point.

The acceleration is caused by a restoring force that always pointing to the mean position and is proportional to the displacement from the mean position.

a = −ω²x

The negative signs signifies that the acceleration is always is always pointing back towards the mean position

4.1.4 Solve problems using the defining equation for SHM.

4.1.5 Apply the equations x = sin(ωt) , v = Aωcos(ωt), a = -Aω² sin(ωt), v =±ω√((A²-x² ) ) as solutions to the defining equation for SHM.

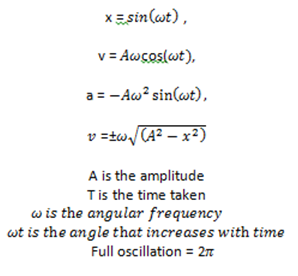
Elastic potential energy E_EP = 1/2 kx²

4.1.6 Solve problems, both graphically and by calculation, for acceleration, velocity and displacement during SHM.